Definitie en soorten systemen van lineaire vergelijkingen. Systemen van lineaire vergelijkingen oplossen

§1. Systemen van lineaire vergelijkingen.

Systeem bekijken

een systeem genoemd M lineaire vergelijkingen met N onbekend.

Hier
- onbekend, - coëfficiënten voor onbekenden,
- vrije termen van de vergelijkingen.

Als alle vrije termen van de vergelijkingen gelijk zijn aan nul, wordt het systeem aangeroepen homogeen.Bij besluit systeem wordt een verzameling getallen genoemd
Wanneer we ze in het systeem vervangen in plaats van onbekenden, veranderen alle vergelijkingen in identiteiten. Het systeem wordt gebeld gewricht, als er minstens één oplossing is. Een compatibel systeem met een unieke oplossing wordt genoemd zeker. De twee systemen worden genoemd equivalent, als de sets van hun oplossingen samenvallen.

Systeem (1) kan in matrixvorm worden weergegeven met behulp van de vergelijking

(2)

.

§2. Compatibiliteit van systemen van lineaire vergelijkingen.

Laten we de uitgebreide matrix van systeem (1) de matrix noemen

Stelling van Kronecker-Capelli. Systeem (1) is consistent als en slechts als de rangorde van de systeemmatrix gelijk is aan de rangorde van de uitgebreide matrix:

.

§3. SysteemoplossingN lineaire vergelijkingen metN onbekend.

Beschouw een inhomogeen systeem N lineaire vergelijkingen met N onbekend:

(3)

De stelling van Cramer.Als de belangrijkste determinant van het systeem (3)
, dan heeft het systeem een ​​unieke oplossing, bepaald door de formules:

die.
,

Waar - determinant verkregen uit de determinant vervanging e kolom naar de kolom met vrije leden.

Als
, en tenminste één van ≠0, dan heeft het systeem geen oplossingen.

Als
, dan heeft het systeem oneindig veel oplossingen.

Systeem (3) kan worden opgelost met behulp van zijn matrixvorm (2). Als de matrixrang A gelijk aan N, d.w.z.
en vervolgens de matrix A heeft een inverse
. De matrixvergelijking vermenigvuldigen
naar de matrix
aan de linkerkant krijgen we:

.

De laatste gelijkheid drukt de methode uit voor het oplossen van stelsels van lineaire vergelijkingen met behulp van een inverse matrix.

Voorbeeld. Los een stelsel vergelijkingen op met behulp van een inverse matrix.

Oplossing. Matrix
niet-gedegenereerd, sindsdien
, wat betekent dat er een inverse matrix is. Laten we de inverse matrix berekenen:
.

,

Oefening. Los het systeem op met behulp van de methode van Cramer.

§4. Willekeurige stelsels van lineaire vergelijkingen oplossen.

Laten we een niet-homogeen systeem van lineaire vergelijkingen van de vorm (1) geven.

Laten we aannemen dat het systeem consistent is, d.w.z. aan de voorwaarde van de stelling van Kronecker-Capelli is voldaan:
. Als de matrixrang
(aantal onbekenden), dan heeft het systeem een ​​unieke oplossing. Als
, dan heeft het systeem oneindig veel oplossingen. Laat het me uitleggen.

Laten we de rangorde van de matrix bepalen R(A)= R< N. Omdat de
, dan is er een minder belangrijke orde dan nul R. Laten we het de basisminor noemen. De onbekenden waarvan de coëfficiënten een basisminor vormen, worden basisvariabelen genoemd. De resterende onbekenden noemen we vrije variabelen. Laten we de vergelijkingen herschikken en de variabelen opnieuw nummeren, zodat deze minor zich in de linkerbovenhoek van de systeemmatrix bevindt:

.

Eerst R lijnen zijn lineair onafhankelijk, de rest wordt daardoor uitgedrukt. Daarom kunnen deze lijnen (vergelijkingen) worden weggegooid. We krijgen:

Laten we de vrije variabelen willekeurige numerieke waarden geven: . Laten we alleen de basisvariabelen aan de linkerkant laten staan ​​en de vrije variabelen naar de rechterkant verplaatsen.

Ik heb het systeem R lineaire vergelijkingen met R onbekend, waarvan de determinant anders is dan 0. Het heeft een unieke oplossing.

Dit systeem wordt de algemene oplossing van het stelsel lineaire vergelijkingen (1) genoemd. Anders: de uitdrukking van basisvariabelen door middel van vrije variabelen wordt genoemd algemeen besluit systemen. Hieruit kun je een oneindig aantal halen particuliere oplossingen, waardoor vrije variabelen willekeurige waarden krijgen. Een specifieke oplossing verkregen uit een algemene oplossing voor nulwaarden van vrije variabelen wordt genoemd basisoplossing. Het aantal verschillende basisoplossingen is niet groter dan
. Een basisoplossing met niet-negatieve componenten wordt genoemd ondersteunen systeem oplossing.

Voorbeeld.

,R=2.

Variabelen
- basis,
- vrij.

Laten we de vergelijkingen bij elkaar optellen; laten we uitdrukken
door
:

- gemeenschappelijk besluit.

- particuliere oplossing voor
.

- basisoplossing, referentie.

§5. Gauss-methode.

De Gauss-methode is een universele methode voor het bestuderen en oplossen van willekeurige systemen van lineaire vergelijkingen. Het bestaat uit het reduceren van het systeem tot een diagonale (of driehoekige) vorm door opeenvolgend onbekenden te elimineren met behulp van elementaire transformaties die de gelijkwaardigheid van systemen niet schenden. Een variabele wordt als uitgesloten beschouwd als deze slechts in één vergelijking van het systeem met een coëfficiënt van 1 voorkomt.

Elementaire transformaties systemen zijn:

Een vergelijking vermenigvuldigen met een ander getal dan nul;

Een vergelijking optellen vermenigvuldigd met een willekeurig getal met een andere vergelijking;

Vergelijkingen herschikken;

Het verwerpen van de vergelijking 0 = 0.

Elementaire transformaties kunnen niet worden uitgevoerd op vergelijkingen, maar op uitgebreide matrices van de resulterende equivalente systemen.

Voorbeeld.

Oplossing. Laten we de uitgebreide matrix van het systeem uitschrijven:

.

Door elementaire transformaties uit te voeren, zullen we de linkerkant van de matrix terugbrengen tot eenheidsvorm: we zullen enen creëren op de hoofddiagonaal en nullen daarbuiten.

Opmerking. Als bij het uitvoeren van elementaire transformaties een vergelijking van de vorm 0 wordt verkregen = k(Waar Naar0), dan is het systeem inconsistent.

De oplossing van systemen van lineaire vergelijkingen door de methode van opeenvolgende eliminatie van onbekenden kan in de vorm worden geschreven tafels.

De linkerkolom van de tabel bevat informatie over uitgesloten (basis)variabelen. De overige kolommen bevatten de coëfficiënten van de onbekenden en de vrije termen van de vergelijkingen.

De uitgebreide matrix van het systeem wordt vastgelegd in de brontabel. Vervolgens beginnen we Jordan-transformaties uit te voeren:

1. Selecteer een variabele , wat de basis zal worden. De bijbehorende kolom wordt de sleutelkolom genoemd. Kies een vergelijking waarin deze variabele blijft bestaan, omdat hij wordt uitgesloten van andere vergelijkingen. De bijbehorende tabelrij wordt een sleutelrij genoemd. Coëfficiënt , die op het kruispunt van een sleutelrij en een sleutelkolom staat, wordt een sleutel genoemd.

2. De sleutelreekselementen zijn onderverdeeld in het sleutelelement.

3. De sleutelkolom is gevuld met nullen.

4. De overige elementen worden berekend met behulp van de rechthoekregel. Maak een rechthoek, op de tegenoverliggende hoekpunten bevindt zich een sleutelelement en een herberekend element; van het product van de elementen op de diagonaal van de rechthoek met het sleutelelement, wordt het product van de elementen van de andere diagonaal afgetrokken en het resulterende verschil gedeeld door het sleutelelement.

Voorbeeld. Vind de algemene oplossing en de basisoplossing van het stelsel vergelijkingen:

Oplossing.

Algemene oplossing van het systeem:

Basisoplossing:
.

Met een enkele substitutietransformatie kunt u van de ene basis van het systeem naar de andere gaan: in plaats van een van de hoofdvariabelen wordt een van de vrije variabelen in de basis geïntroduceerd. Om dit te doen, selecteert u een sleutelelement in de vrije variabelekolom en voert u transformaties uit volgens het bovenstaande algoritme.

§6. Ondersteuningsoplossingen vinden

De referentieoplossing van een stelsel lineaire vergelijkingen is een basisoplossing die geen negatieve componenten bevat.

De referentieoplossingen van het systeem worden gevonden met de Gauss-methode als aan de volgende voorwaarden wordt voldaan.

1. In het oorspronkelijke systeem moeten alle vrije termen niet-negatief zijn:
.

2. Het sleutelelement wordt geselecteerd uit de positieve coëfficiënten.

3. Als een in de basis geïntroduceerde variabele meerdere positieve coëfficiënten heeft, dan is de sleutellijn degene waarin de verhouding tussen de vrije term en de positieve coëfficiënt het kleinst is.

Notitie 1. Als er tijdens het elimineren van onbekenden een vergelijking verschijnt waarin alle coëfficiënten niet-positief zijn en de vrije term zijn
, dan heeft het systeem geen niet-negatieve oplossingen.

Opmerking 2. Als er geen enkel positief element in de kolommen met coëfficiënten voor vrije variabelen staat, is de overgang naar een andere referentieoplossing onmogelijk.

Voorbeeld.

Vergelijkingssystemen worden in de economische sector veel gebruikt voor het wiskundig modelleren van verschillende processen. Bijvoorbeeld bij het oplossen van problemen op het gebied van productiebeheer en -planning, logistieke routes (transportprobleem) of plaatsing van apparatuur.

Vergelijkingssystemen worden niet alleen in de wiskunde gebruikt, maar ook in de natuurkunde, scheikunde en biologie, bij het oplossen van problemen bij het vinden van de populatiegrootte.

Een systeem van lineaire vergelijkingen bestaat uit twee of meer vergelijkingen met verschillende variabelen waarvoor het nodig is een gemeenschappelijke oplossing te vinden. Zo'n reeks getallen waarvoor alle vergelijkingen echte gelijkheden worden of bewijzen dat de reeks niet bestaat.

Lineaire vergelijking

Vergelijkingen van de vorm ax+by=c worden lineair genoemd. De aanduidingen x, y zijn de onbekenden waarvan de waarde moet worden gevonden, b, a zijn de coëfficiënten van de variabelen, c is de vrije term van de vergelijking.
Als u een vergelijking oplost door deze uit te zetten, ziet het eruit als een rechte lijn, waarvan alle punten oplossingen zijn voor de polynoom.

Soorten systemen van lineaire vergelijkingen

De eenvoudigste voorbeelden worden beschouwd als stelsels van lineaire vergelijkingen met twee variabelen X en Y.

F1(x, y) = 0 en F2(x, y) = 0, waarbij F1,2 functies zijn en (x, y) functievariabelen zijn.

Systeem van vergelijkingen oplossen - dit betekent het vinden van waarden (x, y) waarbij het systeem in een echte gelijkheid verandert, of vaststellen dat geschikte waarden van x en y niet bestaan.

Een paar waarden (x, y), geschreven als de coördinaten van een punt, wordt een oplossing voor een stelsel lineaire vergelijkingen genoemd.

Als systemen één gemeenschappelijke oplossing hebben of als er geen oplossing bestaat, worden ze gelijkwaardig genoemd.

Homogene systemen van lineaire vergelijkingen zijn systemen waarvan de rechterkant gelijk is aan nul. Als het rechterdeel na het gelijkteken een waarde heeft of wordt uitgedrukt door een functie, is zo'n systeem heterogeen.

Het aantal variabelen kan veel meer dan twee zijn, dan moeten we het hebben over een voorbeeld van een systeem van lineaire vergelijkingen met drie of meer variabelen.

Wanneer schoolkinderen met systemen worden geconfronteerd, gaan ze ervan uit dat het aantal vergelijkingen noodzakelijkerwijs moet samenvallen met het aantal onbekenden, maar dit is niet het geval. Het aantal vergelijkingen in het systeem is niet afhankelijk van de variabelen; er kunnen er zoveel zijn als gewenst.

Eenvoudige en complexe methoden voor het oplossen van stelsels vergelijkingen

Er bestaat geen algemene analytische methode om dergelijke systemen op te lossen; alle methoden zijn gebaseerd op numerieke oplossingen. De wiskundecursus op school beschrijft in detail methoden als permutatie, algebraïsche optelling, substitutie, evenals grafische en matrixmethoden, oplossing volgens de Gauss-methode.

De belangrijkste taak bij het aanleren van oplossingsmethoden is om te leren hoe je het systeem correct kunt analyseren en voor elk voorbeeld het optimale oplossingsalgoritme kunt vinden. Het belangrijkste is niet om voor elke methode een systeem van regels en acties uit het hoofd te leren, maar om de principes van het gebruik van een bepaalde methode te begrijpen

Het oplossen van voorbeelden van stelsels van lineaire vergelijkingen in het algemene leerplan van groep 7 is vrij eenvoudig en wordt tot in detail uitgelegd. In elk wiskundehandboek krijgt dit gedeelte voldoende aandacht. Het oplossen van voorbeelden van stelsels van lineaire vergelijkingen met behulp van de Gauss- en Cramer-methode wordt in de eerste jaren van het hoger onderwijs nader bestudeerd.

Systemen oplossen met behulp van de substitutiemethode

De acties van de substitutiemethode zijn erop gericht de waarde van de ene variabele uit te drukken in termen van de tweede. De uitdrukking wordt vervangen door de resterende vergelijking en vervolgens gereduceerd tot een vorm met één variabele. De actie wordt herhaald afhankelijk van het aantal onbekenden in het systeem

Laten we een oplossing geven voor een voorbeeld van een systeem van lineaire vergelijkingen van klasse 7 met behulp van de substitutiemethode:

Zoals uit het voorbeeld blijkt, werd de variabele x uitgedrukt via F(X) = 7 + Y. De resulterende uitdrukking, gesubstitueerd in de tweede vergelijking van het systeem in plaats van X, hielp om één variabele Y in de tweede vergelijking te verkrijgen . Het oplossen van dit voorbeeld is eenvoudig en stelt u in staat de Y-waarde te achterhalen. De laatste stap is het controleren van de verkregen waarden.

Het is niet altijd mogelijk om een ​​voorbeeld van een stelsel van lineaire vergelijkingen op te lossen door middel van substitutie. De vergelijkingen kunnen complex zijn en het uitdrukken van de variabele in termen van de tweede onbekende zal te omslachtig zijn voor verdere berekeningen. Als er meer dan 3 onbekenden in het systeem zitten, is oplossen door vervanging ook ongepast.

Oplossing van een voorbeeld van een systeem van lineaire inhomogene vergelijkingen:

Oplossing met behulp van algebraïsche optelling

Bij het zoeken naar oplossingen voor systemen met behulp van de optelmethode, worden vergelijkingen term voor term opgeteld en met verschillende getallen vermenigvuldigd. Het uiteindelijke doel van wiskundige bewerkingen is een vergelijking in één variabele.

Toepassing van deze methode vereist oefening en observatie. Het oplossen van een stelsel lineaire vergelijkingen met behulp van de optellingsmethode als er drie of meer variabelen zijn, is niet eenvoudig. Algebraïsche optelling is handig als vergelijkingen breuken en decimalen bevatten.

Oplossingsalgoritme:

1. Vermenigvuldig beide zijden van de vergelijking met een bepaald getal. Als resultaat van de rekenkundige bewerking moet een van de coëfficiënten van de variabele gelijk worden aan 1.
2. Voeg de resulterende uitdrukking term voor term toe en vind een van de onbekenden.
3. Vervang de resulterende waarde in de tweede vergelijking van het systeem om de resterende variabele te vinden.

Oplossingsmethode door een nieuwe variabele te introduceren

Er kan een nieuwe variabele worden geïntroduceerd als het systeem een ​​oplossing vereist voor niet meer dan twee vergelijkingen;

De methode wordt gebruikt om een ​​van de vergelijkingen te vereenvoudigen door een nieuwe variabele te introduceren. De nieuwe vergelijking wordt opgelost voor het geïntroduceerde onbekende, en de resulterende waarde wordt gebruikt om de oorspronkelijke variabele te bepalen.

Het voorbeeld laat zien dat het door de introductie van een nieuwe variabele t mogelijk was om de eerste vergelijking van het systeem terug te brengen tot een standaard kwadratische trinominaal. Je kunt een polynoom oplossen door de discriminant te vinden.

Het is noodzakelijk om de waarde van de discriminant te vinden met behulp van de bekende formule: D = b2 - 4*a*c, waarbij D de gewenste discriminant is, b, a, c zijn de factoren van de polynoom. In het gegeven voorbeeld is a=1, b=16, c=39, dus D=100. Als de discriminant groter is dan nul, dan zijn er twee oplossingen: t = -b±√D / 2*a, als de discriminant kleiner is dan nul, dan is er één oplossing: x = -b / 2*a.

De oplossing voor de resulterende systemen wordt gevonden door de toevoegingsmethode.

Visuele methode voor het oplossen van systemen

Geschikt voor 3 vergelijkingssystemen. De methode bestaat uit het construeren van grafieken van elke vergelijking in het systeem op de coördinatenas. De coördinaten van de snijpunten van de curven zullen de algemene oplossing van het systeem zijn.

De grafische methode kent een aantal nuances. Laten we verschillende voorbeelden bekijken van het op een visuele manier oplossen van stelsels van lineaire vergelijkingen.

Zoals uit het voorbeeld blijkt, werden voor elke lijn twee punten geconstrueerd, de waarden van de variabele x werden willekeurig gekozen: 0 en 3. Op basis van de waarden van x werden de waarden voor y gevonden: 3 en 0. Punten met coördinaten (0, 3) en (3, 0) zijn gemarkeerd in de grafiek en verbonden door een lijn.

De stappen moeten worden herhaald voor de tweede vergelijking. Het snijpunt van de lijnen is de oplossing van het systeem.

Het volgende voorbeeld vereist het vinden van een grafische oplossing voor een stelsel van lineaire vergelijkingen: 0,5x-y+2=0 en 0,5x-y-1=0.

Zoals uit het voorbeeld blijkt, heeft het systeem geen oplossing, omdat de grafieken evenwijdig zijn en elkaar niet over de gehele lengte snijden.

De systemen uit de voorbeelden 2 en 3 zijn vergelijkbaar, maar wanneer ze worden geconstrueerd, wordt het duidelijk dat hun oplossingen verschillend zijn. Houd er rekening mee dat het niet altijd mogelijk is om te zeggen of een systeem een ​​oplossing heeft of niet; het is altijd nodig om een ​​grafiek te construeren.

De matrix en zijn variëteiten

Matrices worden gebruikt om een ​​systeem van lineaire vergelijkingen beknopt te schrijven. Een matrix is ​​een speciaal soort tabel gevuld met getallen. n*m heeft n - rijen en m - kolommen.

Een matrix is ​​vierkant als het aantal kolommen en rijen gelijk is. Een matrixvector is een matrix van één kolom met een oneindig aantal rijen. Een matrix met enen langs een van de diagonalen en andere nulelementen wordt identiteit genoemd.

Een inverse matrix is ​​een matrix waarmee de oorspronkelijke matrix verandert in een eenheidsmatrix; een dergelijke matrix bestaat alleen voor de oorspronkelijke vierkante matrix.

Regels voor het omzetten van een stelsel vergelijkingen in een matrix

Met betrekking tot stelsels van vergelijkingen worden de coëfficiënten en vrije termen van de vergelijkingen geschreven als matrixgetallen; één vergelijking is één rij van de matrix.

Er wordt gezegd dat een matrixrij niet nul is als ten minste één element van de rij niet nul is. Als het aantal variabelen in een van de vergelijkingen verschilt, is het daarom noodzakelijk om nul in te voeren in plaats van de ontbrekende onbekende.

De matrixkolommen moeten strikt overeenkomen met de variabelen. Dit betekent dat de coëfficiënten van de variabele x slechts in één kolom kunnen worden geschreven, bijvoorbeeld de eerste, de coëfficiënt van de onbekende y - alleen in de tweede.

Bij het vermenigvuldigen van een matrix worden alle elementen van de matrix opeenvolgend vermenigvuldigd met een getal.

Opties voor het vinden van de inverse matrix

De formule voor het vinden van de inverse matrix is ​​vrij eenvoudig: K -1 = 1 / |K|, waarbij K -1 de inverse matrix is, en |K| is de determinant van de matrix. |K| mag niet gelijk zijn aan nul, dan heeft het systeem een ​​oplossing.

De determinant kan eenvoudig worden berekend voor een twee-bij-twee-matrix; u hoeft alleen maar de diagonale elementen met elkaar te vermenigvuldigen. Voor de optie “drie bij drie” is er een formule |K|=a 1 b 2 c 3 + a 1 b 3 c 2 + a 3 b 1 c 2 + a 2 b 3 c 1 + a 2 b 1 c 3 + een 3 b 2 c 1 . U kunt de formule gebruiken, of u kunt onthouden dat u uit elke rij en elke kolom één element moet nemen, zodat het aantal kolommen en rijen met elementen niet in het werk wordt herhaald.

Voorbeelden van stelsels van lineaire vergelijkingen oplossen met behulp van de matrixmethode

Met de matrixmethode voor het vinden van een oplossing kunt u omslachtige invoer verminderen bij het oplossen van systemen met een groot aantal variabelen en vergelijkingen.

In het voorbeeld zijn nm de coëfficiënten van de vergelijkingen, de matrix is ​​een vector, x n zijn variabelen en bn zijn vrije termen.

Systemen oplossen met behulp van de Gaussiaanse methode

In de hogere wiskunde wordt de Gaussiaanse methode samen met de Cramer-methode bestudeerd, en het proces van het vinden van oplossingen voor systemen wordt de Gauss-Cramer-oplossingsmethode genoemd. Deze methoden worden gebruikt om variabelen te vinden van systemen met een groot aantal lineaire vergelijkingen.

De Gauss-methode lijkt sterk op oplossingen door substitutie en algebraïsche optelling, maar is systematischer. In de schoolcursus wordt de oplossing volgens de Gaussische methode gebruikt voor stelsels van 3- en 4-vergelijkingen. Het doel van de methode is om het systeem terug te brengen tot de vorm van een omgekeerd trapezium. Door middel van algebraïsche transformaties en substituties wordt de waarde van één variabele gevonden in een van de vergelijkingen van het systeem. De tweede vergelijking is een uitdrukking met 2 onbekenden, terwijl 3 en 4 respectievelijk 3 en 4 variabelen zijn.

Nadat het systeem in de beschreven vorm is gebracht, wordt de verdere oplossing gereduceerd tot de opeenvolgende vervanging van bekende variabelen in de vergelijkingen van het systeem.

In schoolboeken voor groep 7 wordt een voorbeeld van een oplossing volgens de Gauss-methode als volgt beschreven:

Zoals uit het voorbeeld blijkt, werden bij stap (3) twee vergelijkingen verkregen: 3x 3 -2x 4 =11 en 3x 3 +2x 4 =7. Door een van de vergelijkingen op te lossen, kun je een van de variabelen x n ontdekken.

Stelling 5, die in de tekst wordt genoemd, stelt dat als een van de vergelijkingen van het systeem wordt vervangen door een equivalent, het resulterende systeem ook equivalent zal zijn aan het oorspronkelijke.

De Gaussiaanse methode is moeilijk te begrijpen voor middelbare scholieren, maar het is een van de meest interessante manieren om de vindingrijkheid te ontwikkelen van kinderen die zijn ingeschreven voor geavanceerde leerprogramma's in wiskunde- en natuurkundelessen.

Om de registratie te vergemakkelijken, worden de berekeningen meestal als volgt uitgevoerd:

De coëfficiënten van de vergelijkingen en vrije termen worden geschreven in de vorm van een matrix, waarbij elke rij van de matrix overeenkomt met een van de vergelijkingen van het systeem. scheidt de linkerkant van de vergelijking van de rechterkant. Romeinse cijfers geven het aantal vergelijkingen in het systeem aan.

Schrijf eerst de matrix op waarmee u wilt werken en vervolgens alle acties die met een van de rijen worden uitgevoerd. De resulterende matrix wordt na het "pijl" -teken geschreven en de noodzakelijke algebraïsche bewerkingen worden voortgezet totdat het resultaat is bereikt.

Het resultaat zou een matrix moeten zijn waarin een van de diagonalen gelijk is aan 1 en alle andere coëfficiënten gelijk zijn aan nul, dat wil zeggen dat de matrix wordt gereduceerd tot een eenheidsvorm. We mogen niet vergeten berekeningen uit te voeren met getallen aan beide kanten van de vergelijking.

Deze opnamemethode is minder omslachtig en zorgt ervoor dat u niet wordt afgeleid door het opsommen van talloze onbekende zaken.

Het gratis gebruik van elke oplossingsmethode vereist zorg en enige ervaring. Niet alle methoden zijn van toegepaste aard. Sommige methoden om oplossingen te vinden verdienen meer de voorkeur op een bepaald gebied van menselijke activiteit, terwijl andere voor educatieve doeleinden bestaan.

Het bestuderen van een systeem van lineaire leeftijdsgebonden vergelijkingen (SLAE's) op consistentie betekent uitzoeken of dit systeem oplossingen heeft of niet. Welnu, als er oplossingen zijn, geef dan aan hoeveel er zijn.

We hebben informatie nodig over het onderwerp "Systeem van lineaire algebraïsche vergelijkingen. Basistermen. Matrixvorm van notatie". In het bijzonder zijn concepten als systeemmatrix en uitgebreide systeemmatrix nodig, aangezien de formulering van de stelling van Kronecker-Capelli daarop is gebaseerd. Zoals gebruikelijk zullen we de systeemmatrix aanduiden met de letter $A$, en de uitgebreide matrix van het systeem met de letter $\widetilde(A)$.

Stelling van Kronecker-Capelli

Een systeem van lineaire algebraïsche vergelijkingen is consistent als en slechts als de rangorde van de systeemmatrix gelijk is aan de rangorde van de uitgebreide matrix van het systeem, d.w.z. $\rang A=\rang\widetilde(A)$.

Ik wil u eraan herinneren dat een systeem gezamenlijk wordt genoemd als het ten minste één oplossing heeft. De stelling van Kronecker-Capelli zegt dit: als $\rang A=\rang\widetilde(A)$, dan is er een oplossing; als $\rang A\neq\rang\widetilde(A)$, dan heeft deze SLAE geen oplossingen (inconsistent). Het antwoord op de vraag over het aantal van deze oplossingen wordt gegeven door een uitvloeisel van de stelling van Kronecker-Capelli. Bij het formuleren van het uitvloeisel wordt de letter $n$ gebruikt, die gelijk is aan het aantal variabelen van de gegeven SLAE.

Uitvloeisel van de stelling van Kronecker-Capelli

1. Als $\rang A\neq\rang\widetilde(A)$, dan is de SLAE inconsistent (heeft geen oplossingen).
2. Als $\rang A=\rang\widetilde(A)< n$, то СЛАУ является неопределённой (имеет бесконечное количество решений).
3. Als $\rang A=\rang\widetilde(A) = n$, dan is de SLAE definitief (heeft precies één oplossing).

Houd er rekening mee dat de geformuleerde stelling en het uitvloeisel daarvan niet aangeven hoe een oplossing voor de SLAE moet worden gevonden. Met hun hulp kun je er alleen achter komen of deze oplossingen bestaan ​​of niet, en als ze bestaan, hoeveel dan.

Voorbeeld nr. 1

Ontdek SLAE $ \left \(\begin(uitgelijnd) & -3x_1+9x_2-7x_3=17;\\ & -x_1+2x_2-4x_3=9;\\ & 4x_1-2x_2+19x_3=-42. \end(uitgelijnd )\right.$ voor compatibiliteit. Als de SLAE compatibel is, geef dan het aantal oplossingen aan.

Om het bestaan ​​van oplossingen voor een gegeven SLAE te achterhalen, gebruiken we de stelling van Kronecker-Capelli. We hebben de matrix van het systeem $A$ en de uitgebreide matrix van het systeem $\widetilde(A)$ nodig, we zullen ze schrijven:

$$ A=\left(\begin(matrix) (ccc) -3 & 9 & -7 \\ -1 & 2 & -4 \\ 4 & -2 & 19 \end(matrix) \right);\; \widetilde(A)=\left(\begin(array) (ccc|c) -3 & 9 &-7 & 17 \\ -1 & 2 & -4 & 9\\ 4 & -2 & 19 & -42 \end(array) \right). $$

We moeten $\rang A$ en $\rang\widetilde(A)$ vinden. Er zijn veel manieren om dit te doen, waarvan sommige worden vermeld in de sectie Matrixrang. Meestal worden twee methoden gebruikt om dergelijke systemen te bestuderen: “Het per definitie berekenen van de rangorde van een matrix” of “Het berekenen van de rangorde van een matrix volgens de methode van elementaire transformaties”.

Methode nummer 1. Computers behoren per definitie tot de top.

Volgens de definitie is rang de hoogste orde van de minoren van een matrix, waaronder er minstens één is die verschilt van nul. Meestal begint de studie met minoren van de eerste orde, maar hier is het handiger om meteen te beginnen met het berekenen van de minor van de derde orde van de matrix $A$. De secundaire elementen van de derde orde bevinden zich op het snijpunt van drie rijen en drie kolommen van de betreffende matrix. Omdat de matrix $A$ slechts 3 rijen en 3 kolommen bevat, is de derde orde minor van de matrix $A$ de determinant van de matrix $A$, d.w.z. $\Delta A$. Om de determinant te berekenen, passen we formule nr. 2 toe uit het onderwerp "Formules voor het berekenen van determinanten van de tweede en derde orde":

$$ \Delta A=\links| \begin(matrix) (ccc) -3 & 9 & -7 \\ -1 & 2 & -4 \\ 4 & -2 & 19 \end(matrix) \right|=-21. $$

Er is dus een derde orde minor van de matrix $A$, die niet gelijk is aan nul. Het is onmogelijk om een ​​minor van de vierde orde te construeren, omdat deze 4 rijen en 4 kolommen vereist, en de matrix $A$ slechts 3 rijen en 3 kolommen heeft. Dus de hoogste orde van de minoren van de matrix $A$, waarvan er tenminste één is die niet gelijk is aan nul, is gelijk aan 3. Daarom is $\rang A=3$.

We moeten ook $\rang\widetilde(A)$ vinden. Laten we eens kijken naar de structuur van de matrix $\widetilde(A)$. Tot aan de regel in de matrix $\widetilde(A)$ zijn er elementen van de matrix $A$, en we kwamen erachter dat $\Delta A\neq 0$. De matrix $\widetilde(A)$ heeft dus een minor van de derde orde, die niet gelijk is aan nul. We kunnen geen minoren van de vierde orde construeren van de matrix $\widetilde(A)$, dus concluderen we: $\rang\widetilde(A)=3$.

Omdat $\rang A=\rang\widetilde(A)$, is het systeem volgens de stelling van Kronecker-Capelli consistent, d.w.z. heeft een oplossing (minstens één). Om het aantal oplossingen aan te geven houden we er rekening mee dat onze SLAE 3 onbekenden bevat: $x_1$, $x_2$ en $x_3$. Omdat het aantal onbekenden $n=3$ is, concluderen we: $\rang A=\rang\widetilde(A)=n$, daarom is het systeem, volgens het uitvloeisel van de stelling van Kronecker-Capelli, definitief, d.w.z. heeft een unieke oplossing.

Het probleem is opgelost. Welke nadelen en voordelen heeft deze methode? Laten we het eerst hebben over de voordelen. Ten eerste hoefden we slechts één determinant te vinden. Hierna hebben we direct een conclusie getrokken over het aantal oplossingen. Normaal gesproken geven standaard standaardberekeningen stelsels van vergelijkingen die drie onbekenden bevatten en een unieke oplossing hebben. Voor dergelijke systemen is deze methode erg handig, omdat we van tevoren weten dat er een oplossing is (anders had het voorbeeld niet in de standaardberekening gestaan). Die. Het enige wat we moeten doen is op de snelste manier het bestaan ​​van een oplossing aantonen. Ten tweede zal de berekende waarde van de determinant van de systeemmatrix (dat wil zeggen $\Delta A$) later nuttig zijn: wanneer we een bepaald systeem beginnen op te lossen met behulp van de Cramer-methode of met behulp van de inverse matrix.

De methode voor het berekenen van de rangorde is echter per definitie onwenselijk als de matrix van het systeem $A$ rechthoekig is. In dit geval is het beter om de tweede methode te gebruiken, die hieronder zal worden besproken. Bovendien, als $\Delta A=0$, kunnen we niets zeggen over het aantal oplossingen van een gegeven inhomogene SLAE. Misschien heeft de SLAE een oneindig aantal oplossingen, of misschien geen. Als $\Delta A=0$ is aanvullend onderzoek nodig, wat vaak omslachtig is.

Om samen te vatten wat er is gezegd, merk ik op dat de eerste methode goed is voor die SLAE's waarvan de systeemmatrix vierkant is. Bovendien bevat de SLAE zelf drie of vier onbekenden en is deze ontleend aan standaard standaardberekeningen of tests.

Methode nummer 2. Berekening van rang volgens de methode van elementaire transformaties.

Deze methode wordt gedetailleerd beschreven in het betreffende onderwerp. We beginnen met het berekenen van de rangorde van de matrix $\widetilde(A)$. Waarom matrices $\widetilde(A)$ en niet $A$? Het feit is dat de matrix $A$ deel uitmaakt van de matrix $\widetilde(A)$. Door de rangorde van de matrix $\widetilde(A)$ te berekenen, zullen we daarom tegelijkertijd de rangorde van de matrix $A$ vinden .

\begin(uitgelijnd) &\widetilde(A) =\left(\begin(array) (ccc|c) -3 & 9 &-7 & 17 \\ -1 & 2 & -4 & 9\\ 4 & - 2 & 19 & -42 \end(array) \right) \rightarrow \left|\text(verwissel de eerste en tweede regel)\right| \pijl naar rechts \\ &\pijl naar rechts \left(\begin(array) (ccc|c) -1 & 2 & -4 & 9 \\ -3 & 9 &-7 & 17\\ 4 & -2 & 19 & - 42 \end(array) \right) \begin(array) (l) \phantom(0) \\ II-3\cdot I\\ III+4\cdot I \end(array) \rechterpijl \left(\begin (matrix) (ccc|c) -1 & 2 & -4 & 9 \\ 0 & 3 &5 & -10\\ 0 & 6 & 3 & -6 \end(matrix) \right) \begin(matrix) ( l) \phantom(0) \\ \phantom(0)\\ III-2\cdot II \end(array)\pijl naar rechts\\ &\pijl naar rechts \left(\begin(array) (ccc|c) -1 & 2 & -4 & 9 \\ 0 & 3 &5 & -10\\ 0 & 0 & -7 & 14 \end(array) \right) \end(uitgelijnd)

We hebben de matrix $\widetilde(A)$ teruggebracht tot een trapeziumvorm. Op de hoofddiagonaal van de resulterende matrix $\left(\begin(array) (ccc|c) -1 & 2 & -4 & 9 \\ 0 & 3 &5 & -10\\ 0 & 0 & -7 & 14 \end( array) \right)$ bevat drie elementen die niet nul zijn: -1, 3 en -7. Conclusie: de rangorde van de matrix $\widetilde(A)$ is 3, d.w.z. $\rang\widetilde(A)=3$. Bij het maken van transformaties met de elementen van de matrix $\widetilde(A)$, transformeerden we tegelijkertijd de elementen van de matrix $A$ die zich tot aan de lijn bevonden. De matrix $A$ wordt ook gereduceerd tot een trapeziumvorm: $\left(\begin(array) (ccc) -1 & 2 & -4 \\ 0 & 3 &5 \\ 0 & 0 & -7 \end(array) \rechts)$. Conclusie: de rangorde van matrix $A$ is ook 3, d.w.z. $\rang A=3$.

Omdat $\rang A=\rang\widetilde(A)$, is het systeem volgens de stelling van Kronecker-Capelli consistent, d.w.z. heeft een oplossing. Om het aantal oplossingen aan te geven houden we er rekening mee dat onze SLAE 3 onbekenden bevat: $x_1$, $x_2$ en $x_3$. Omdat het aantal onbekenden $n=3$ is, concluderen we: $\rang A=\rang\widetilde(A)=n$, daarom is het systeem volgens het uitvloeisel van de stelling van Kronecker-Capelli gedefinieerd, d.w.z. heeft een unieke oplossing.

Wat zijn de voordelen van de tweede methode? Het belangrijkste voordeel is de veelzijdigheid. Het maakt voor ons niet uit of de matrix van het systeem vierkant is of niet. Bovendien hebben we daadwerkelijk voorwaartse transformaties van de Gauss-methode uitgevoerd. Er zijn nog maar een paar stappen over en we kunnen een oplossing voor deze SLAE vinden. Eerlijk gezegd vind ik de tweede methode leuker dan de eerste, maar de keuze is een kwestie van smaak.

Antwoord: De gegeven SLAE is consistent en gedefinieerd.

Voorbeeld nr. 2

Ontdek SLAE $ \left\( \begin(uitgelijnd) & x_1-x_2+2x_3=-1;\\ & -x_1+2x_2-3x_3=3;\\ & 2x_1-x_2+3x_3=2;\\ & 3x_1- 2x_2+5x_3=1;\\ & 2x_1-3x_2+5x_3=-4 \end(uitgelijnd) \right.$ voor compatibiliteit.

We zullen de rangen van de systeemmatrix en de uitgebreide systeemmatrix vinden met behulp van de methode van elementaire transformaties. Uitgebreide systeemmatrix: $\widetilde(A)=\left(\begin(array) (ccc|c) 1 & -1 & 2 & -1\\ -1 & 2 & -3 & 3 \\ 2 & -1 & 3 & 2 \\ 3 & -2 & 5 & 1 \\ 2 & -3 & 5 & -4 \end(array) \right)$. Laten we de vereiste rangen vinden door de uitgebreide matrix van het systeem te transformeren:

De uitgebreide matrix van het systeem wordt teruggebracht tot een stapsgewijze vorm. Als een matrix wordt gereduceerd tot een echelonvorm, is de rangorde gelijk aan het aantal rijen die niet nul zijn. Daarom $\rang A=3$. De matrix $A$ (tot aan de lijn) is gereduceerd tot een trapeziumvormige vorm en heeft de rangorde 2, $\rang A=2$.

Omdat $\rang A\neq\rang\widetilde(A)$, is het systeem volgens de stelling van Kronecker-Capelli inconsistent (dat wil zeggen: het heeft geen oplossingen).

Antwoord: Het systeem is inconsistent.

Voorbeeld nr. 3

SLAE verkennen $ \left\( \begin(uitgelijnd) & 2x_1+7x_3-5x_4+11x_5=42;\\ & x_1-2x_2+3x_3+2x_5=17;\\ & -3x_1+9x_2-11x_3-7x_5=-64 ;\\ & -5x_1+17x_2-16x_3-5x_4-4x_5=-90;\\ & 7x_1-17x_2+23x_3+15x_5=132.

De uitgebreide matrix van het systeem heeft de vorm: $\widetilde(A)=\left(\begin(array) (ccccc|c) 2 & 0 & 7 & -5 & 11 & 42\\ 1 & -2 & 3 & 0 & 2 & 17 \\ -3 & 9 & -11 & 0 & -7 & -64 \\ -5 & 17 & -16 & -5 & -4 & -90 \\ 7 & -17 & 23 & 0 & 15 & 132 \end(array) \right)$. Laten we de eerste en tweede rij van deze matrix omwisselen, zodat het eerste element van de eerste rij één wordt: $\left(\begin(array) (ccccc|c) 1 & -2 & 3 & 0 & 2 & 17\\ 2 & 0 & 7 & -5 & 11 & 42 \\ -3 & 9 & -11 & 0 & -7 & -64 \\ -5 & 17 & -16 & -5 & -4 & -90 \\ 7 & -17 & 23 & 0 & 15 & 132 \end(array) \right)$.

We hebben de uitgebreide matrix van het systeem en de matrix van het systeem zelf teruggebracht tot een trapeziumvorm. De rang van de uitgebreide matrix van het systeem is gelijk aan drie, de rang van de matrix van het systeem is ook gelijk aan drie. Omdat het systeem $n=5$ onbekenden bevat, d.w.z. $\rang\widetilde(A)=\rang A< n$, то согласно следствия из теоремы Кронекера-Капелли данная система является неопределённой, т.е. имеет бесконечное количество решений.

Antwoord: Het systeem is onzeker.

In het tweede deel zullen we voorbeelden analyseren die vaak zijn opgenomen in standaardberekeningen of tests in de hogere wiskunde: consistentieonderzoek en oplossing van SLAE afhankelijk van de waarden van de parameters die erin zijn opgenomen.

Een systeem van m lineaire vergelijkingen met n onbekenden een systeem van de vorm genoemd

Waar een IJ En b ik (i=1,…,M; B=1,…,N) zijn enkele bekende nummers, en x 1 ,…,x n- onbekend. Bij de aanduiding van coëfficiënten een IJ eerste index i geeft het vergelijkingsnummer aan, en de tweede J– het getal van het onbekende waarbij deze coëfficiënt staat.

We zullen de coëfficiënten voor de onbekenden in de vorm van een matrix schrijven 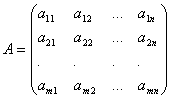, die we zullen bellen matrix van het systeem.

De getallen aan de rechterkant van de vergelijkingen zijn b 1 ,…,b m worden genoemd gratis leden.

Totaliteit N cijfers c 1 ,…,c n genaamd beslissing van een bepaald systeem, als elke vergelijking van het systeem een ​​gelijkheid wordt nadat er getallen in zijn vervangen c 1 ,…,c n in plaats van de overeenkomstige onbekenden x 1 ,…,x n.

Onze taak zal zijn om oplossingen voor het systeem te vinden. In dit geval kunnen zich drie situaties voordoen:

Een stelsel van lineaire vergelijkingen dat minstens één oplossing heeft, wordt genoemd gewricht. Anders, d.w.z. als het systeem geen oplossingen heeft, wordt het aangeroepen niet-gezamenlijk.

Laten we manieren overwegen om oplossingen voor het systeem te vinden.

MATRIXMETHODE VOOR HET OPLOSSEN VAN SYSTEMEN VAN LINEAIRE VERGELIJKINGEN

Matrices maken het mogelijk om in het kort een stelsel van lineaire vergelijkingen op te schrijven. Laat een stelsel van 3 vergelijkingen met drie onbekenden gegeven worden:

Beschouw de systeemmatrix 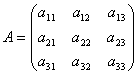en matriceskolommen met onbekende en vrije termen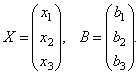

Laten we het werk vinden

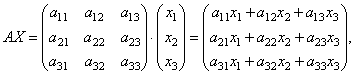
die. als resultaat van het product verkrijgen we de linkerkanten van de vergelijkingen van dit systeem. Vervolgens kan dit systeem, met behulp van de definitie van matrixgelijkheid, in de vorm worden geschreven

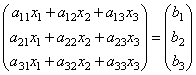of korter A∙X=B.

Hier zijn de matrixen A En B bekend zijn, en de matrix X onbekend. Het is noodzakelijk om het te vinden, omdat... de elementen ervan zijn de oplossing voor dit systeem. Deze vergelijking wordt genoemd matrixvergelijking.

Laat de determinant van de matrix verschillend zijn van nul | A| ≠ 0. Vervolgens wordt de matrixvergelijking als volgt opgelost. Vermenigvuldig beide zijden van de vergelijking aan de linkerkant met de matrix A-1, omgekeerd van de matrix A: . Omdat de EEN -1 EEN = E En E∙X = X, dan verkrijgen we een oplossing voor de matrixvergelijking in de vorm X = A -1 B .

Merk op dat aangezien de inverse matrix alleen kan worden gevonden voor vierkante matrices, de matrixmethode alleen die systemen kan oplossen waarin het aantal vergelijkingen valt samen met het aantal onbekenden. Matrixregistratie van het systeem is echter ook mogelijk in het geval dat het aantal vergelijkingen niet gelijk is aan het aantal onbekenden, dan wordt de matrix A zal niet vierkant zijn en daarom is het onmogelijk om in de vorm een ​​oplossing voor het systeem te vinden X = A -1 B.

Voorbeelden. Systemen van vergelijkingen oplossen.

CRAMER'S REGEL

Beschouw een systeem van 3 lineaire vergelijkingen met drie onbekenden:

Derde orde determinant die overeenkomt met de systeemmatrix, d.w.z. samengesteld uit coëfficiënten voor onbekenden,

genaamd bepalend voor het systeem.

Laten we nog drie determinanten als volgt samenstellen: vervang achtereenvolgens 1, 2 en 3 kolommen in de determinant D door een kolom met vrije termen

Dan kunnen we het volgende resultaat bewijzen.

Stelling (regel van Cramer). Als de determinant van het systeem Δ ≠ 0, dan heeft het beschouwde systeem slechts één oplossing, en

Bewijs. Laten we dus een systeem van drie vergelijkingen met drie onbekenden bekijken. Laten we de eerste vergelijking van het systeem vermenigvuldigen met het algebraïsche complement Een 11 element een 11, 2e vergelijking – aan Een 21 en 3e – aan Een 31:

Laten we deze vergelijkingen toevoegen:

Laten we naar elk van de haakjes en de rechterkant van deze vergelijking kijken. Door de stelling over de uitbreiding van de determinant in elementen van de 1e kolom

Op dezelfde manier kan worden aangetoond dat en .

Ten slotte is het gemakkelijk om dat op te merken

We verkrijgen dus de gelijkheid: .

Vandaar, .

De gelijkheden en zijn op dezelfde manier afgeleid, waaruit de verklaring van de stelling volgt.

We merken dus op dat als de determinant van het systeem Δ ≠ 0 is, het systeem een ​​unieke oplossing heeft en omgekeerd. Als de determinant van het systeem gelijk is aan nul, dan heeft het systeem óf een oneindig aantal oplossingen, óf geen oplossingen, d.w.z. onverenigbaar.

Voorbeelden. Systeem van vergelijkingen oplossen

GAUSS-METHODE

De eerder besproken methoden kunnen alleen worden gebruikt om die systemen op te lossen waarin het aantal vergelijkingen samenvalt met het aantal onbekenden, en de determinant van het systeem verschillend moet zijn van nul. De Gauss-methode is universeler en geschikt voor systemen met een willekeurig aantal vergelijkingen. Het bestaat uit de consistente eliminatie van onbekenden uit de vergelijkingen van het systeem.

Beschouw opnieuw een systeem van drie vergelijkingen met drie onbekenden:

.

We laten de eerste vergelijking ongewijzigd, en vanaf de 2e en 3e sluiten we de termen uit die deze bevatten x 1. Om dit te doen, deelt u de tweede vergelijking door A 21 en vermenigvuldig met – A 11, en tel dit vervolgens op bij de eerste vergelijking. Op dezelfde manier delen we de derde vergelijking door A 31 en vermenigvuldig met – A 11, en voeg het dan toe met de eerste. Als gevolg hiervan zal het oorspronkelijke systeem de vorm aannemen:

Nu elimineren we uit de laatste vergelijking de term bevattende x 2. Om dit te doen, deelt u de derde vergelijking door, vermenigvuldigt u met en telt u op met de tweede. Dan hebben we een stelsel vergelijkingen:

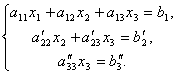
Vanaf hier is het gemakkelijk te vinden vanaf de laatste vergelijking x 3, en vervolgens uit de tweede vergelijking x 2 en tenslotte, van 1e - x 1.

Bij gebruik van de Gaussische methode kunnen de vergelijkingen indien nodig worden verwisseld.

Vaak beperken ze zich, in plaats van een nieuw systeem van vergelijkingen te schrijven, tot het uitschrijven van de uitgebreide matrix van het systeem:

en breng het vervolgens naar een driehoekige of diagonale vorm met behulp van elementaire transformaties.

NAAR elementaire transformaties matrices omvatten de volgende transformaties:

1. het herschikken van rijen of kolommen;
2. een string vermenigvuldigen met een ander getal dan nul;
3. andere regels aan één regel toevoegen.

Voorbeelden: Los stelsels vergelijkingen op met behulp van de Gauss-methode.

Het systeem heeft dus een oneindig aantal oplossingen.

Laten we eerst het geval bekijken waarin het aantal vergelijkingen gelijk is aan het aantal variabelen, d.w.z. m = n. Dan is de matrix van het systeem vierkant en wordt de determinant ervan de determinant van het systeem genoemd.

Inverse matrixmethode

Laten we in algemene vorm het stelsel vergelijkingen AX = B bekijken met een niet-gedegenereerde vierkante matrix A. In dit geval is er een inverse matrix A -1. Laten we beide zijden vermenigvuldigen met A -1 aan de linkerkant. We krijgen A -1 AX = A -1 B. Dus EX = A -1 B en

De laatste gelijkheid is een matrixformule voor het vinden van oplossingen voor dergelijke stelsels vergelijkingen. Het gebruik van deze formule wordt de inverse matrixmethode genoemd

Laten we deze methode bijvoorbeeld gebruiken om het volgende systeem op te lossen:

;

Aan het einde van het oplossen van het systeem kunt u dit controleren door de gevonden waarden in de systeemvergelijkingen te vervangen. Daarbij moeten ze veranderen in echte gelijkheid.

Laten we voor het beschouwde voorbeeld het volgende controleren:

Methode voor het oplossen van stelsels van lineaire vergelijkingen met een vierkante matrix met behulp van de formules van Cramer

Stel n= 2:

Als we beide zijden van de eerste vergelijking vermenigvuldigen met a 22, en beide zijden van de tweede met (-a 12), en vervolgens de resulterende vergelijkingen optellen, dan elimineren we de variabele x 2 uit het systeem. Op dezelfde manier kunt u de variabele x 1 elimineren (door beide zijden van de eerste vergelijking te vermenigvuldigen met (-a 21), en beide zijden van de tweede met 11). Als resultaat krijgen we het systeem:

De uitdrukking tussen haakjes is de determinant van het systeem

Laten we aanduiden

Het systeem zal dan de vorm aannemen:

Uit het resulterende systeem volgt dat als de determinant van het systeem 0 is, het systeem consistent en definitief zal zijn. De enige oplossing kan worden berekend met behulp van de formules:

Als = 0, a 1 0 en/of  2 0, dan hebben de systeemvergelijkingen de vorm 0*x 1 = 2 en/of 0*x 1 = 2. In dit geval zal het systeem inconsistent zijn.

In het geval dat = 1 = 2 = 0, zal het systeem consistent en onbepaald zijn (zal een oneindig aantal oplossingen hebben), aangezien het de vorm zal aannemen:

De stelling van Cramer(we laten het bewijs achterwege). Als de determinant van de matrix van een stelsel vergelijkingen  niet gelijk is aan nul, dan heeft het systeem een ​​unieke oplossing, bepaald door de formules:

,

waarbij  j de determinant is van de matrix die wordt verkregen uit matrix A door de j-de kolom te vervangen door een kolom met vrije termen.

De bovenstaande formules worden genoemd Cramer-formules.

Laten we als voorbeeld deze methode gebruiken om een ​​systeem op te lossen dat eerder werd opgelost met behulp van de inverse matrixmethode:

Nadelen van de overwogen methoden:

1) significante arbeidsintensiteit (determinanten berekenen en de inverse matrix vinden);

2) beperkte reikwijdte (voor systemen met een vierkante matrix).

Echte economische situaties worden vaak gemodelleerd door systemen waarin het aantal vergelijkingen en variabelen behoorlijk groot is, en er meer vergelijkingen zijn dan variabelen. Daarom is de volgende methode in de praktijk gebruikelijker.

Gaussiaanse methode (methode voor opeenvolgende eliminatie van variabelen)

Deze methode wordt gebruikt om een ​​stelsel van m lineaire vergelijkingen met n variabelen in algemene vorm op te lossen. De essentie ervan ligt in het toepassen van een systeem van gelijkwaardige transformaties op de uitgebreide matrix, met behulp waarvan het systeem van vergelijkingen wordt getransformeerd naar een vorm waarin de oplossingen ervan gemakkelijk te vinden worden (indien aanwezig).

Dit is een weergave waarin het gedeelte linksboven van de systeemmatrix een getrapte matrix zal zijn. Dit wordt bereikt met behulp van dezelfde technieken die werden gebruikt om een ​​stappenmatrix te verkrijgen om de rangorde te bepalen. In dit geval worden elementaire transformaties toegepast op de uitgebreide matrix, waardoor een gelijkwaardig systeem van vergelijkingen kan worden verkregen. Hierna zal de uitgebreide matrix de vorm aannemen:

Het verkrijgen van zo’n matrix heet rechtdoorzee Gauss-methode.

Het vinden van de waarden van variabelen uit het overeenkomstige stelsel van vergelijkingen wordt genoemd omgekeerd Gauss-methode. Laten we het overwegen.

Merk op dat de laatste (m – r) vergelijkingen de vorm zullen aannemen:

Als ten minste één van de cijfers
niet gelijk is aan nul, dan zal de overeenkomstige gelijkheid onwaar zijn en zal het hele systeem inconsistent zijn.

Daarom voor elk gezamenlijk systeem
. In dit geval zijn de laatste (m – r) vergelijkingen voor alle waarden van de variabelen de identiteit 0 = 0, en deze kunnen worden genegeerd bij het oplossen van het systeem (gooi eenvoudigweg de overeenkomstige rijen weg).

Hierna ziet het systeem er als volgt uit:

Laten we eerst het geval bekijken waarin r=n. Het systeem zal dan de vorm aannemen:

Uit de laatste vergelijking van het systeem kan xr op unieke wijze worden gevonden.

Als we x r kennen, kunnen we er ondubbelzinnig x r -1 uit uitdrukken. Vervolgens kunnen we uit de vorige vergelijking, als we x r en x r -1 kennen, x r -2 uitdrukken, enz. tot x1.

In dit geval zal het systeem dus gezamenlijk en gedefinieerd zijn.

Beschouw nu het geval waarin r eenvoudig(hoofd), en al de rest - niet-fundamenteel(niet-kern, gratis). De laatste vergelijking van het systeem zal zijn:

Uit deze vergelijking kunnen we de basisvariabele x r uitdrukken in termen van niet-basisvariabelen:

De voorlaatste vergelijking ziet er als volgt uit:

Door de resulterende uitdrukking daarin te vervangen in plaats van x r, zal het mogelijk zijn de basisvariabele x r -1 uit te drukken in termen van niet-basisvariabelen. Enz. naar variabelex 1 . Om een ​​oplossing voor het systeem te verkrijgen, kunt u niet-basisvariabelen gelijkstellen aan willekeurige waarden en vervolgens de basisvariabelen berekenen met behulp van de resulterende formules. In dit geval zal het systeem dus consistent en onbepaald zijn (een oneindig aantal oplossingen hebben).

Laten we bijvoorbeeld het stelsel vergelijkingen oplossen:

We zullen de verzameling basisvariabelen noemen basis systemen. We zullen hiervoor ook de reeks kolommen met coëfficiënten noemen basis(basiskolommen), of basis minor systeemmatrices. De oplossing van het systeem waarin alle niet-basisvariabelen gelijk zijn aan nul wordt aangeroepen basisoplossing.

In het vorige voorbeeld is de basisoplossing (4/5; -17/5; 0; 0) (de variabelen x 3 en x 4 (c 1 en c 2) zijn ingesteld op nul, en de basisvariabelen x 1 en x 2 worden hierdoor berekend). Om een ​​voorbeeld te geven van een niet-basisoplossing, moeten we x 3 en x 4 (c 1 en c 2) gelijkstellen aan willekeurige getallen die niet tegelijkertijd nul zijn, en de resterende variabelen daardoor berekenen. Met 1 = 1 en 2 = 0 krijgen we bijvoorbeeld een niet-basisoplossing - (4/5; -12/5; 1; 0). Door substitutie is het eenvoudig om te verifiëren dat beide oplossingen correct zijn.

Het is duidelijk dat er in een onbepaald systeem een ​​oneindig aantal niet-basisoplossingen kan zijn. Hoeveel basisoplossingen zijn er mogelijk? Elke rij van de getransformeerde matrix moet overeenkomen met één basisvariabele. Er zijn n variabelen in het probleem, en r basislijnen. Daarom kan het aantal van alle mogelijke sets basisvariabelen niet groter zijn dan het aantal combinaties van n bij 2. Het kan minder zijn dan , omdat het niet altijd mogelijk is om het systeem in een zodanige vorm te transformeren dat deze specifieke reeks variabelen de basis vormt.

Wat voor soort is dit? Dit is het type waarbij de matrix gevormd uit kolommen met coëfficiënten voor deze variabelen getrapt zal zijn en tegelijkertijd uit r rijen zal bestaan. Die. de rangorde van de coëfficiëntenmatrix voor deze variabelen moet gelijk zijn aan r. Het kan niet groter zijn, omdat het aantal kolommen gelijk is. Als deze kleiner blijkt te zijn dan r, duidt dit op een lineaire afhankelijkheid van de kolommen van de variabelen. Dergelijke kolommen kunnen geen basis vormen.

Laten we eens kijken welke andere basisoplossingen er in het hierboven besproken voorbeeld te vinden zijn. Om dit te doen, overweeg alle mogelijke combinaties van vier variabelen met twee basisvariabelen. Er zullen dergelijke combinaties zijn
, en een daarvan (x 1 en x 2) is al overwogen.

Laten we de variabelen x 1 en x 3 nemen. Laten we de rangorde van de matrix van coëfficiënten voor hen vinden:

Omdat het gelijk is aan twee, kunnen ze eenvoudig zijn. Laten we de niet-basisvariabelen x 2 en x 4 gelijkstellen aan nul: x 2 = x 4 = 0. Dan volgt uit de formule x 1 = 4/5 – (1/5)*x 4 dat x 1 = 4 /5, en uit de formule x 2 = -17/5 + x 3 - - (7/5)*x 4 = -17/5 + x 3 volgt dat x 3 = x 2 +17/5 = 17/ 5. We krijgen dus de basisoplossing (4/5; 0; 17/5; 0).

Op dezelfde manier kunt u basisoplossingen verkrijgen voor de basisvariabelen x 1 en x 4 – (9/7; 0; 0; -17/7); x 2 en x 4 – (0; -9; 0; 4); x 3 en x 4 – (0; 0; 9; 4).

De variabelen x 2 en x 3 in dit voorbeeld kunnen niet als basisvariabelen worden beschouwd, omdat de rangorde van de overeenkomstige matrix gelijk is aan één, d.w.z. minder dan twee:

.

Een andere benadering om te bepalen of het al dan niet mogelijk is om op basis van bepaalde variabelen een basis te construeren, is ook mogelijk. Bij het oplossen van het voorbeeld, als resultaat van het converteren van de systeemmatrix naar een stapsgewijze vorm, nam het de vorm aan:

Door paren variabelen te selecteren, was het mogelijk om de overeenkomstige minoren van deze matrix te berekenen. Het is gemakkelijk te verifiëren dat ze voor alle paren behalve x 2 en x 3 niet gelijk zijn aan nul, d.w.z. de kolommen zijn lineair onafhankelijk. En alleen voor kolommen met variabelen x 2 en x 3
, wat hun lineaire afhankelijkheid aangeeft.

Laten we naar een ander voorbeeld kijken. Laten we het stelsel vergelijkingen oplossen

De vergelijking die overeenkomt met de derde rij van de laatste matrix is ​​dus tegenstrijdig - deze resulteerde in de onjuiste gelijkheid 0 = -1, daarom is dit systeem inconsistent.

Jordan-Gauss-methode 3 is een ontwikkeling van de Gaussische methode. De essentie ervan is dat de uitgebreide matrix van het systeem wordt getransformeerd naar een vorm waarin de coëfficiënten van de variabelen een identiteitsmatrix vormen tot aan de permutatie van rijen of kolommen 4 (waarbij r de rangorde van de systeemmatrix is).

Laten we het systeem oplossen met behulp van deze methode:

Laten we eens kijken naar de uitgebreide matrix van het systeem:

In deze matrix selecteren we een eenheidselement. De coëfficiënt voor x 2 in de derde beperking is bijvoorbeeld 5. Laten we ervoor zorgen dat de resterende rijen in deze kolom nullen bevatten, d.w.z. Laten we de kolom enkelvoudig maken. Tijdens het transformatieproces zullen we dit noemen kolomtolerant(leidend, sleutel). De derde beperking (derde lijn) wij bellen ook tolerant. Mezelf element, dat op het snijpunt van de oplossende rij en kolom staat (hier is het er één), wordt ook wel genoemd tolerant.

De eerste regel bevat nu de coëfficiënt (-1). Om een ​​nul op zijn plaats te krijgen, vermenigvuldigt u de derde regel met (-1) en trekt u het resultaat af van de eerste regel (dat wil zeggen: u voegt eenvoudigweg de eerste regel toe aan de derde).

De tweede regel bevat de coëfficiënt 2. Om nul op zijn plaats te krijgen, vermenigvuldigt u de derde regel met 2 en trekt u het resultaat af van de eerste regel.

Het resultaat van de transformatie ziet er als volgt uit:

Uit deze matrix is ​​duidelijk zichtbaar dat één van de eerste twee restricties kan worden doorgestreept (de corresponderende rijen zijn proportioneel, d.w.z. deze vergelijkingen volgen uit elkaar). Laten we bijvoorbeeld de tweede doorstrepen:

Het nieuwe systeem heeft dus twee vergelijkingen. Er wordt één enkele kolom (tweede) verkregen en de eenheid verschijnt hier in de tweede rij. Laten we niet vergeten dat de tweede vergelijking van het nieuwe systeem zal overeenkomen met de basisvariabele x 2.

Laten we een basisvariabele voor de eerste rij kiezen. Dit kan elke variabele zijn behalve x 3 (omdat voor x 3 de eerste beperking een coëfficiënt nul heeft, d.w.z. de reeks variabelen x 2 en x 3 kan hier niet fundamenteel zijn). U kunt de eerste of de vierde variabele nemen.

Laten we x 1 kiezen. Het oplossende element is dan 5, en beide zijden van de oplossende vergelijking moeten door vijf worden gedeeld om er één in de eerste kolom van de eerste rij te krijgen.

Laten we ervoor zorgen dat de resterende rijen (dat wil zeggen de tweede rij) nullen hebben in de eerste kolom. Omdat de tweede regel nu niet nul bevat, maar 3, moeten we van de tweede regel de elementen van de getransformeerde eerste regel aftrekken, vermenigvuldigd met 3:

Uit de resulterende matrix kan men direct één basisoplossing extraheren door niet-basisvariabelen gelijk te stellen aan nul, en basisvariabelen aan de vrije termen in de overeenkomstige vergelijkingen: (0,8; -3,4; 0; 0). Je kunt ook algemene formules afleiden die basisvariabelen uitdrukken via niet-basisvariabelen: x 1 = 0,8 – 1,2 x 4; x 2 = -3,4 + x 3 + 1,6 x 4. Deze formules beschrijven de volledige oneindige reeks oplossingen voor het systeem (door x 3 en x 4 gelijk te stellen aan willekeurige getallen, kun je x 1 en x 2 berekenen).

Merk op dat de essentie van de transformaties in elke fase van de Jordan-Gauss-methode als volgt was:

1) de resolutielijn werd gedeeld door het resolutie-element om in plaats daarvan een eenheid te verkrijgen,

2) Van alle andere rijen werd het getransformeerde oplossende element afgetrokken, vermenigvuldigd met het element dat zich op de gegeven regel in de oplossende kolom bevond, om een ​​nul te verkrijgen in plaats van dit element.

Laten we opnieuw de getransformeerde uitgebreide matrix van het systeem bekijken:

Uit dit record blijkt duidelijk dat de rangorde van de matrix van systeem A gelijk is aan r.

In de loop van onze redenering hebben we vastgesteld dat het systeem alleen dan coöperatief zal zijn als
. Dit betekent dat de uitgebreide matrix van het systeem er als volgt uit zal zien:

Door nul rijen weg te gooien, verkrijgen we dat de rangorde van de uitgebreide matrix van het systeem ook gelijk is aan r.

Stelling van Kronecker-Capelli. Een systeem van lineaire vergelijkingen is consistent als en slechts als de rangorde van de matrix van het systeem gelijk is aan de rangorde van de uitgebreide matrix van dit systeem.

Bedenk dat de rangorde van een matrix gelijk is aan het maximale aantal lineair onafhankelijke rijen. Hieruit volgt dat als de rangorde van de uitgebreide matrix kleiner is dan het aantal vergelijkingen, de vergelijkingen van het systeem lineair afhankelijk zijn en dat een of meer daarvan uit het systeem kunnen worden uitgesloten (aangezien ze lineair zijn). combinatie van de anderen). Een stelsel vergelijkingen zal alleen lineair onafhankelijk zijn als de rangorde van de uitgebreide matrix gelijk is aan het aantal vergelijkingen.

Bovendien kan voor gelijktijdige systemen van lineaire vergelijkingen worden beargumenteerd dat als de rangorde van de matrix gelijk is aan het aantal variabelen, het systeem een ​​unieke oplossing heeft, en als deze kleiner is dan het aantal variabelen, dan het systeem is onbepaald en heeft oneindig veel oplossingen.

1 Stel dat er bijvoorbeeld vijf rijen in de matrix zijn (de oorspronkelijke rijvolgorde is 12345). We moeten de tweede regel en de vijfde veranderen. Om ervoor te zorgen dat de tweede regel de plaats van de vijfde inneemt en naar beneden "beweegt", veranderen we achtereenvolgens de aangrenzende lijnen drie keer: de tweede en derde (13245), de tweede en vierde (13425) en de tweede en vijfde (13452). ). Om ervoor te zorgen dat de vijfde rij de plaats van de tweede in de oorspronkelijke matrix inneemt, is het vervolgens noodzakelijk om de vijfde rij met slechts twee opeenvolgende wijzigingen naar boven te “verschuiven”: de vijfde en vierde rij (13542) en de vijfde en derde rij. (15342).

2Aantal combinaties van n tot r ze noemen het aantal van alle verschillende r-element-subsets van een n-element-set (degenen met verschillende samenstellingen van elementen worden als verschillende sets beschouwd; de volgorde van selectie is niet belangrijk). Het wordt berekend met behulp van de formule:
. Laten we ons de betekenis van het teken “!” herinneren (faculteit):
0!=1.)

3 Omdat deze methode gebruikelijker is dan de eerder besproken Gaussische methode, en in wezen een combinatie is van de voorwaartse en achterwaartse stappen van de Gaussische methode, wordt deze ook wel de Gaussische methode genoemd, waarbij het eerste deel van de naam wordt weggelaten.

4Bijvoorbeeld
.

5Als er geen eenheden in de systeemmatrix zouden zijn, zou het bijvoorbeeld mogelijk zijn om beide zijden van de eerste vergelijking door twee te delen, en dan zou de eerste coëfficiënt eenheid worden; of iets dergelijks