次の場合、数値 r は行列 A のランクと呼ばれます。
1) 行列 A にはゼロとは異なる次数 r のマイナーが存在します。
2) 次数 (r+1) 以上のすべてのマイナーが存在する場合、それらはゼロに等しい。
それ以外の場合、行列のランクはゼロ以外の最高の副次数になります。
指定: rangA、r A または r。
定義から、r は正の整数であることがわかります。 ヌル行列の場合、ランクはゼロとみなされます。
サービスの目的。 オンライン計算機は、次のことを見つけるように設計されています。 マトリックスランク。 この場合、ソリューションは Word および Excel 形式で保存されます。 解決策の例を参照してください。
説明書。 マトリックスの次元を選択し、「次へ」をクリックします。
意味 。 ランク r の行列が与えられるとします。 ゼロとは異なり次数 r を持つ行列のマイナーは基本と呼ばれ、そのコンポーネントの行と列は基本行と基本列と呼ばれます。
この定義によれば、行列 A は複数の基底マイナーを持つことができます。
単位行列 E のランクは n (行数) です。
例1. 2 つの行列が与えられると、 
およびその未成年者 
, 
。 どれが基本的なものとして考えられますか?
解決。 マイナー M 1 =0 なので、どの行列の基礎にもなりません。 マイナー M 2 =-9≠0 で次数は 2 です。つまり、ランクが 2 に等しい場合、行列 A または / および B の基底として使用できます。 detB=0 (2 つの比例列を持つ行列式として) であるため、rangB=2 および M 2 を行列 B の基底副次関数として取得できます。 detA=-27≠ であるため、行列 A のランクは 3 です。 0 であるため、この行列の基底マイナー次数は 3 に等しくなければなりません。つまり、M 2 は行列 A の基底ではありません。 行列 A には、行列 A の行列式に等しい単一基底マイナーがあることに注意してください。
定理（基底マイナーについて）。
行列の行 (列) は、その基本行 (列) の線形結合です。
定理からの帰結。
- ランク r のすべての (r+1) 列 (行) 行列は線形従属です。
- 行列のランクがその行 (列) の数より小さい場合、その行 (列) は線形依存します。 rangA がその行 (列) の数と等しい場合、行 (列) は線形に独立しています。
- 行列 A の行列式は、その行 (列) が線形従属している場合に限り、ゼロに等しくなります。
- 行列の行 (列) に別の行 (列) を追加し、ゼロ以外の数値を乗算しても、行列の順位は変わりません。
- 他の行 (列) の線形結合である行列の行 (列) を取り消しても、行列のランクは変わりません。
- 行列のランクは、線形に独立した行 (列) の最大数に等しくなります。
- 線形独立行の最大数は、線形独立列の最大数と同じです。
例2。 行列の順位を求める 
.
解決。
マトリックス ランクの定義に基づいて、ゼロとは異なる最高次数のマイナーを探します。 まず、行列をより単純な形式に変換しましょう。 これを行うには、行列の最初の行に (-2) を乗算して 2 番目の行に加算し、次に (-1) を乗算して 3 番目の行に加算します。
いくつかの行列を与えてみましょう:
.
このマトリックスで選択しましょう 
任意の文字列と 
任意の列 
。 それから決定要因は 
行列要素で構成される次数 
、選択した行と列の交点に位置し、マイナーと呼ばれます 
二次行列 
.
定義 1.13.マトリックスランク 
は、この行列の非ゼロのマイナーの最大次数です。
行列のランクを計算するには、その最低次数のすべてのマイナーを考慮し、それらの少なくとも 1 つが 0 以外の場合は、最高次数のマイナーの検討に進む必要があります。 マトリックスのランクを決定するこのアプローチは、境界法 (または境界マイナー法) と呼ばれます。
問題1.4。マイナー境界法を使用して、マトリックスのランクを決定します 
.
.
たとえば、次のような 1 次エッジ化を考えてみましょう。 
。 次に、二次エッジングの検討に進みます。
例えば、 
.
最後に、3次境界を分析してみましょう。
.
したがって、ゼロ以外のマイナーの最高次数は 2 です。 
.
問題 1.4 を解くと、多くの 2 次境界マイナーがゼロではないことがわかります。 これに関して、次の概念が適用されます。
定義 1.14.行列の基底マイナーは、次数が行列のランクと等しい非ゼロのマイナーです。
定理1.2。(基底定理)。 基底行 (基底列) は線形に独立しています。
行列の行 (列) は、そのうちの少なくとも 1 つが他の行 (列) の線形結合として表現できる場合に限り、線形従属であることに注意してください。
定理1.3。線形独立行列の行の数は、線形独立行列の列の数に等しく、行列のランクに等しい。
定理1.4。(行列式がゼロになるための必要十分条件)。 決め手となるためには 
-番目の注文 
がゼロに等しい場合、その行 (列) が線形に依存していることが必要かつ十分です。
行列の定義に基づいて行列のランクを計算するのは非常に面倒です。 これは、高次の行列の場合に特に重要になります。 この点に関して、実際には、行列のランクは、定理 10.2 ～ 10.4 の適用、および行列の等価性と基本変換の概念の使用に基づいて計算されます。
定義 1.15. 2 つの行列 
そして 
それらのランクが等しい場合、つまり同等であると呼ばれます。 
.
行列の場合 
そして 
は同等である場合は、注意してください 
.
定理1.5。行列のランクは、基本的な変換によって変化しません。
基本的な行列変換を呼びます 
行列に対する次の操作のいずれか:
行を列に置き換え、列を対応する行に置き換えます。
行列の行を再配置します。
要素がすべてゼロである行を取り消す。
文字列にゼロ以外の数値を乗算する。
ある行の要素に、別の行の対応する要素を同じ数値で乗算して追加します。 
.
定理 1.5 の帰結。マトリックスの場合 
マトリックスから得られる 
有限数の基本変換を使用して、行列 
そして 
は同等です。
行列のランクを計算するときは、有限数の基本変換を使用して台形形に縮小する必要があります。
定義1.16。台形を、ゼロ以外の最高次の境界マイナーで、対角要素より下のすべての要素が消えるときの行列表現の形式と呼びます。 例えば：
.
ここ 
、行列要素 
ゼロに行きます。 この場合、そのような行列の表現形式は台形になります。
通常、行列はガウス アルゴリズムを使用して台形に縮小されます。 ガウス アルゴリズムの考え方は、行列の最初の行の要素に対応する係数を乗算することで、その要素の下にある最初の列のすべての要素が得られるというものです。 
、ゼロになります。 次に、2 番目の列の要素に対応する係数を乗算して、2 番目の列のすべての要素がその要素の下にあることを確認します。 
、ゼロになります。 その後、同じように進めます。
問題1.5。行列を台形に縮小して行列のランクを決定します。
.
ガウス アルゴリズムを使いやすくするために、1 行目と 3 行目を入れ替えることができます。
.
ここでは明らかです 
。 ただし、結果をより洗練された形式にするために、列の変換をさらに続けることができます。
.
また、このトピックの重要な実践的な応用についても検討します。 一貫性のための連立一次方程式の研究.
マトリックスのランクは何ですか?
記事のユーモラスなエピグラフには多くの真実が含まれています。 私たちは通常、「ランク」という言葉をある種の階層、最も多くの場合はキャリアのはしごを連想します。 知識、経験、能力、人脈などがあればあるほど。 – 彼の地位と機会の範囲が高くなります。 若者用語でのランクとは、一般的な「険しさ」の度合いを指します。
そして私たちの数学的な兄弟たちは同じ原則に従って生きています。 ランダムにいくつか散歩に出かけましょう ゼロ行列:
マトリックスで考えてみましょう すべてゼロ, では何位の話ができるのでしょうか？ 「トータルゼロ」という非公式な表現は誰もがよく知っています。 行列社会では、すべてがまったく同じです。
ゼロ行列のランクどのサイズもゼロに等しい.
注記 : ゼロ行列はギリシャ文字「シータ」で表されます。
マトリックスのランクをよりよく理解するために、以下では役立つ資料を使用します。 解析幾何学。 ゼロを考える ベクター私たちの三次元空間は、特定の方向を定めず、建築には役に立たない アフィン基底。 代数の観点から、このベクトルの座標は次のように書かれます。 マトリックス「1つずつ」と論理的 (示された幾何学的意味で)この行列のランクがゼロであると仮定します。
では、いくつか見てみましょう ゼロ以外の 列ベクトルそして 行ベクトル:
各インスタンスには少なくとも 1 つの非ゼロ要素があり、それは何かです。
ゼロ以外の行ベクトル (列ベクトル) のランクは 1 に等しくなります。
そして一般的に言えば、 マトリックス内にある場合 任意のサイズ少なくとも 1 つの非ゼロ要素があり、そのランクがある それ以下ではない単位.
代数的な行ベクトルと列ベクトルはある程度抽象的であるため、幾何学的な関連付けに戻りましょう。 ゼロ以外の ベクター空間に非常に明確な方向を設定し、構築に適しています。 基礎したがって、行列のランクは 1 に等しいと見なされます。
理論情報 : 線形代数では、ベクトルはベクトル空間 (8 つの公理によって定義される) の要素であり、特に、定義された実数による加算と乗算の演算を使用して、実数の順序付けられた行 (または列) を表すことができます。彼らのために。 ベクターの詳細については、記事を参照してください。 線形変換.
線形依存性（お互いを通して表現します）。 幾何学的観点から見ると、2 行目には共線ベクトルの座標が含まれます。 
、それは問題を構築する上でまったく前進しませんでした 三次元基底、この意味では余分です。 したがって、この行列のランクも 1 に等しくなります。
ベクトルの座標を列に書き換えてみましょう ( 行列を転置する):
ランク的には何が変わったのでしょうか？ 何もない。 列は比例しており、ランクが 1 に等しいことを意味します。 ちなみに、3 つの直線もすべて比例していることに注意してください。 座標で識別できる 三つ平面の共線ベクトル、そのうち 唯一「フラットな」基礎を構築するのに役立ちます。 そしてこれは、私たちの幾何学的ランクの感覚と完全に一致しています。
上記の例から重要なステートメントが続きます。
行列の行のランクは行列の列のランクと同じです。 これについては、効果的なレッスンですでに少し触れました。 行列式を計算する方法.
注記 : 行の線形依存性は、列の線形依存性を意味します (逆も同様)。 ただし、時間を節約するために、また習慣から、私はほとんどの場合、文字列の線形依存性について話します。
大切なペットのしつけを続けていきましょう。 別の共線ベクトルの座標を 3 行目の行列に追加してみましょう 
:
彼は私たちが三次元の基礎を構築するのを手伝ってくれましたか？ もちろん違います。 3 つのベクトルはすべて同じパスに沿って行き来し、行列のランクは 1 に等しくなります。 共線ベクトルを好きなだけ (たとえば 100 個) 取得し、それらの座標を「100 x 3」行列に入れることができますが、そのような超高層ビルのランクは 1 のままです。
マトリックスについて見てみましょう。その行は 線形独立。 非共線ベクトルのペアは、3 次元の基底を構築するのに適しています。 この行列のランクは 2 です。
マトリックスのランクは何ですか? 線は比例していないようです...つまり、理論的には 3 つです。 ただし、この行列のランクも 2 です。 最初の 2 行を追加し、その結果を最後に書きました。 直線的に表現される 3 行目から最初の 2 行まで。 幾何学的には、行列の行は 3 つの座標に対応します。 同一平面上のベクトル、そしてこの3人の中には共線性のない仲間が2人います。
ご覧のように、 線形依存性考慮されたマトリックスでは明らかではないため、今日はそれを公にする方法を学びます。
マトリックスのランクが何であるかを推測できる人は多いと思います。
次の行を持つ行列を考えてみましょう。 線形独立。 ベクトル形式 アフィン基底、この行列のランクは 3 です。
ご存知のとおり、3 次元空間の 4 番目、5 番目、10 番目のベクトルは基底ベクトルに関して線形に表現されます。 したがって、行列に任意の数の行を追加すると、そのランクは 依然として 3 に等しくなります.
同様の推論は、より大きなサイズの行列に対しても実行できます (もちろん、幾何学的意味はありません)。
意味 : 行列のランクは線形に独立した行の最大数です。 または： 行列のランクは線形に独立した列の最大数です。 はい、その番号は常に同じです。
上記のことから、重要な実践的なガイドラインも得られます。 行列のランクは最小次元を超えない。 たとえば、マトリックスでは 
4 行 5 列。 最小次元は 4 であるため、この行列のランクが 4 を超えることはありません。
指定: 世界の理論と実践では、行列のランクを指定するための一般に受け入れられた標準はありません; ほとんどの場合、次のことがわかります: - よく言われるように、イギリス人はあることを書き、ドイツ人は別のことを書きます。 したがって、アメリカとロシアの地獄についての有名なジョークに基づいて、行列のランクをネイティブの単語で表してみましょう。 例えば： 。 そして、行列が「名前なし」である場合（多数ある）、単純に と書くことができます。
マイナーを使用して行列のランクを見つけるにはどうすればよいですか?
私の祖母が行列に 5 番目の列を持っていた場合、彼女は 4 次の別のマイナー (「青」、「ラズベリー」 + 5 番目の列) を計算する必要があります。
結論: ゼロ以外のマイナーの最大次数は 3 で、これは を意味します。
おそらく誰もがこのフレーズを完全に理解しているわけではありません。4 次のマイナーはゼロに等しいですが、3 次のマイナーの中にはゼロでないものがあり、したがって最大次数になります。 ゼロ以外のマイナーで 3 に相当します。
なぜすぐに行列式を計算しないのかという疑問が生じます。 第一に、ほとんどのタスクでは行列は正方ではありません。第二に、たとえゼロ以外の値を取得したとしても、通常は標準的な「ボトムアップ」ソリューションが必要となるため、タスクは拒否される可能性が高くなります。 そして、考慮した例では、4 次のゼロ行列式により、行列のランクが 4 未満に過ぎないと述べることができます。
正直に言うと、未成年者との境界線を定める方法をよりよく説明するために、私が自分で分析したこの問題を思いつきました。 実際には、すべてはもっと単純です。
例 2
エッジマイナー法を使用して行列のランクを見つける 
解答と答えはレッスンの最後にあります。
アルゴリズムが最も速く動作するのはいつですか? 同じ 4 行 4 列の行列に戻りましょう。 
。 明らかに、「良い」場合の解決策は最短になります。 コーナーマイナー:
そして、 if 、 then 、それ以外の場合 – 。
この考え方はまったく仮説的なものではありません。問題全体が角度マイナーのみに限定されている例はたくさんあります。
ただし、場合によっては、別の方法の方が効果的で好ましい場合があります。
ガウス法を使用して行列のランクを見つけるにはどうすればよいですか?
この段落は、すでに に精通している読者を対象としています。 ガウス法そして多かれ少なかれ彼らは彼を手に入れました。
技術的な観点から見ると、この方法は目新しいものではありません。
1) 基本変換を使用して、行列を段階的な形式に縮小します。
2) 行列のランクは行数に等しい。
それは絶対に明らかです ガウス法を使用しても行列のランクは変わりません、そしてここでの本質は非常に単純です。アルゴリズムによれば、基本的な変換中に、すべての不要な比例（線形依存）行が識別されて削除され、その結果、線形独立行の最大数である「乾燥残差」が生じます。
3 つの共線ベクトルの座標を使用して、昔からよく知られている行列を変換してみましょう。 
(1) 1 行目は 2 行目に加算され、-2 が乗算されます。 1行目が3行目に追加されました。
(2) ゼロ行は削除されます。
したがって、1 行が残っているため、 になります。 言うまでもなく、これは、2 次のゼロマイナーを 9 個計算して初めて結論を出すよりもはるかに高速です。
それ自体を思い出させてください 代数行列何も変更することはできず、変換はランクを決定する目的のみで実行されます。 ところで、なぜそうしないのかという質問についてもう一度考えてみましょう。 ソース行列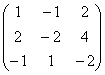 
行列や行の情報とは根本的に異なる情報を運びます。 一部の数学モデルでは (誇張ではありませんが)、1 つの数値の違いが生死に関わる可能性があります。 ...私は、アルゴリズムのわずかな不正確さや逸脱のために、容赦なく成績を 1 ～ 2 ポイント減点した小中学校の数学教師を思い出しました。 そして、一見保証された「A」ではなく、「良い」、あるいはそれ以上の結果になったときは、非常に残念でした。 人工衛星、核弾頭、発電所を人間に任せるにはどうすればよいかという理解が得られたのはずっと後になってからでした。 でも心配しないでください、私はこれらの分野では働いていません =)
より有意義なタスクに移りましょう。そこでは、特に重要な計算技術について学びます。 ガウス法:
例 3
初等変換を使用して行列のランクを求める 
解決: 「4 × 5」行列が与えられます。これは、そのランクが確かに 4 以下であることを意味します。
最初の列には 1 または -1 がないため、少なくとも 1 つのユニットを取得するには追加のアクションが必要です。 サイトの存在を通じて、私は「基本的な変換中に列を再配置することは可能ですか?」という質問を繰り返し受けてきました。 ここでは、1 列目と 2 列目を再配置しました。すべて問題ありません。 ほとんどのタスクで使用されます ガウス法、実際に列を再配置することができます。 しかし、必要ありません。 そして、重要なのは、変数との混同の可能性さえありません。重要なのは、高等数学の古典的なコースでは、このアクションは伝統的に考慮されていないため、そのようなうなずきは非常に曲がった見方で見られる（またはすべてをやり直すことを強いられることさえある）ということです。
2点目は数字に関するものです。 決定を下す際には、次の経験則を使用すると役立ちます。 基本的な変換では、可能であれば行列の数を減らす必要があります。。 結局のところ、たとえば 23、45、97 を使用するよりも、1、2、3 を使用する方がはるかに簡単です。そして、最初のアクションは、最初の列で 1 を取得するだけでなく、数字を削除することも目的としています。 7と11。
最初に完全なソリューションを示し、次にコメントします。 
(1) 1 行目は 2 行目に加算され、-2 が乗算されます。 1 行目は 3 行目に追加され、-3 が乗算されます。 そしてヒープへ: 1 行目は 4 行目に追加され、-1 が乗算されます。
(2) 最後の 3 行は比例です。 3行目と4行目が削除され、2行目が最初の場所に移動されました。
(3) 1 行目は 2 行目に加算され、-3 が乗算されます。
エシェロン形式に縮小された行列には 2 つの行があります。
答え:
次は、4 行 4 列の行列を拷問する番です。
例 4
ガウス法を使用して行列のランクを求める 
私はあなたにそれを思い出させます ガウス法明確な厳格性を意味するものではなく、あなたの決定は私の決定とは異なる可能性が高くなります。 レッスンの最後にあるタスクの簡単な例。
行列のランクを見つけるにはどの方法を使用すればよいですか?
実際には、ランクを見つけるためにどの方法を使用する必要があるかがまったく示されていないことがよくあります。 このような状況では、条件を分析する必要があります。一部の行列ではマイナー関数を使用して解く方が合理的ですが、他の行列では初等変換を適用する方がはるかに有益です。
例5
行列の順位を求める 
解決: 最初のメソッドはどういうわけかすぐに消えてしまいます =)
もう少し詳しく言えば、行列の列に触れないようにアドバイスしましたが、ゼロ列、または比例/一致する列がある場合でも、切断する価値があります。 
(1) 5 番目の列はゼロなので、行列から削除します。 したがって、マトリックスのランクは 4 つ以下です。 最初の行には -1 が乗算されています。 これはガウス法のもう 1 つの特徴的な機能であり、次のアクションを楽しい散歩に変えます。
(2) 2行目以降の全行に1行目を追加しました。
(3) 1 行目は -1 倍、3 行目は 2 で除算、4 行目は 3 で除算されます。2 行目は 5 行目に加算され、-1 倍されます。
(4) 3 行目は 5 行目に加算され、-2 が乗算されます。
(5) 最後の 2 行は比例し、5 行目は削除されます。
結果は4行になります。
答え:
自由研究のための標準的な5階建ての建物:
例6
行列の順位を求める
レッスンの最後に短い解答と答えが表示されます。
「行列ランク」というフレーズは実際にはあまり見られず、ほとんどの問題ではまったく使わなくても問題ないことに注意してください。 ただし、問題の概念が主役となるタスクが 1 つあります。この記事の締めくくりに、この実用的なアプリケーションを紹介します。
連立一次方程式の一貫性を調べるにはどうすればよいでしょうか?
多くの場合、解決策に加えて、 連立一次方程式条件に応じて、まず互換性を調べる必要があります。つまり、何らかの解決策が存在することを証明する必要があります。 このような検証において重要な役割を果たすのは、 クロネッカー・カペリの定理、これを必要な形式で定式化します。
ランクなら システム行列ランクに等しい 拡張マトリックスシステムの場合、システムは一貫しており、この数が未知数の数と一致する場合、解は一意になります。
したがって、システムの互換性を検討するには、同等性をチェックする必要があります。 
、 どこ - システムマトリックス(レッスンで出た用語を思い出してください ガウス法)、A - 拡張システムマトリックス(つまり、変数の係数を含む行列 + 自由項の列)。
小学校次の行列変換が呼び出されます。
1) 任意の 2 つの行 (または列) の順列、
2) 行 (または列) にゼロ以外の数値を乗算します。
3) ある行 (または列) に別の行 (または列) を加算し、特定の数を掛けます。
2 つの行列は次のように呼ばれます。 同等、有限セットの基本変換を使用して、一方が他方から取得される場合。
一般に、等価行列は等しいわけではありませんが、ランクは等しいです。 行列 A と B が等しい場合、A ~ B のように記述されます。
正規行列は、主対角線の先頭に複数の 1 が連続して存在し (その数はゼロでも構いません)、他のすべての要素はゼロに等しい行列です。たとえば、次のようになります。
行と列の基本的な変換を使用すると、あらゆる行列を正規化することができます。 正準行列のランクは、その主対角線上の 1 の数に等しくなります。
例 2行列の順位を求める
A= 
そしてそれを正規の形式に戻します。
解決。 2 行目から最初の行を減算し、次の行を並べ替えます。
.
次に、2 行目と 3 行目から最初の行を減算し、それぞれ 2 と 5 を掛けます。
;
3 行目から最初の行を減算します。 行列を取得します
B = 
,
これは、基本変換の有限セットを使用して行列 A から取得されるため、行列 A と同等です。 明らかに、行列 B のランクは 2 なので、r(A)=2 になります。 行列 B は簡単に正規化できます。 適切な数値を掛けた最初の列を後続のすべての列から減算すると、最初の行を除く最初の行のすべての要素がゼロになり、残りの行の要素は変わりません。 次に、適切な数値を掛けた 2 番目の列を後続のすべての列から減算し、2 番目を除く 2 番目の行のすべての要素をゼロにし、正準行列を取得します。
.
クロネッカー - カペリの定理- 線形代数方程式系の互換性基準:
線形システムが一貫性を保つためには、このシステムの拡張行列のランクがそのメイン行列のランクと等しいことが必要かつ十分です。
証明（システム互換性条件）
必要性
させて システムジョイント 次に、 のような数字があります。 したがって、列は行列の列の線形結合になります。 他の行（列）の線形結合である行（列）の系から行（列）が削除または追加されても行列のランクは変わらないという事実から、次のことがわかります。
適切性
させて 。 マトリックスの基本的なマイナーをいくつか取り上げてみましょう。 したがって、それはマトリックスの基底マイナーにもなります。 すると、基底定理によれば、 マイナーの場合、行列の最後の列は、基底列、つまり行列の列の線形結合になります。 したがって、システムの自由項の列は、行列の列の線形結合になります。
結果
主な変数の数 システムシステムのランクと同じです。
ジョイント システムシステムのランクがそのすべての変数の数と等しい場合、 は定義されます (その解は一意です)。
同次方程式系
オファー15 . 2 同次方程式系
|
|
常に共同です。
証拠。 このシステムの場合、数値セット 、 、 、が解となります。
このセクションでは、システムの行列表記を使用します。
オファー15 . 3 同次一次方程式系の解の和は、この系の解になります。 解に数値を掛けたものも解です。
証拠。 それらをシステムのソリューションとして機能させましょう。 それから、そして。 させて 。 それから
以来、解決策です。
を任意の数としましょう。 それから
以来、解決策です。
結果15 . 1 同次一次方程式系にゼロ以外の解がある場合、無限に多くの異なる解が存在します。
実際、ゼロ以外の解にさまざまな数値を乗算すると、さまざまな解が得られます。
意味15
.
5
解決策は次のようになります。 
システムフォーム 解決の基本システム、列の場合 
は線形独立システムを形成しており、システムの解はこれらの列の線形結合になります。
意味。 マトリックスランクベクトルとしてみなされる線形独立行の最大数です。
行列のランクに関する定理 1。 マトリックスランクは行列の非ゼロマイナーの最大次数と呼ばれます。
マイナーの概念については行列式のレッスンですでに説明しましたが、ここでそれを一般化します。 行列内の特定の行数と特定の列数を考えてみましょう。この「どのくらい」は行列の行と列の数よりも小さくなければなりません。また、行と列の場合、この「いくつ」は次のようになります。同じ番号です。 次に、行数と列数の交差点に、元の行列よりも低次の行列が存在します。 行列式は行列であり、前述の「一部」(行と列の数) が k で示されている場合、k 次のマイナーになります。
意味。マイナー ( r+1) 次のオーダー、その中に選択されたマイナーが含まれます r-th オーダーは、特定のマイナーのボーダーリングと呼ばれます。
最も一般的に使用される 2 つの方法は次のとおりです。 行列の順位を求める。 これ 未成年者との国境の接し方そして 初等変換の方法(ガウス法)。
境界マイナー法を使用する場合、次の定理が使用されます。
行列のランクに関する定理 2。マイナーが行列要素から構成できる場合 r次数がゼロに等しくない場合、行列のランクは次と等しくなります。 r.
基本変換メソッドを使用する場合、次のプロパティが使用されます。
基本的な変換を通じて、元の行列と同等の台形行列が得られた場合、 この行列のランク完全にゼロで構成される行以外の行の数です。
マイナー境界法を使用して行列のランクを求める
囲んでいるマイナーは、この高次のマイナーに指定されたマイナーが含まれている場合、指定されたマイナーに対して相対的に高次のマイナーです。
たとえば、行列が与えられたとすると、
未成年者を連れて行きましょう
境界未成年者は次のとおりです。
行列の順位を求めるアルゴリズム次。
1. ゼロに等しくない 2 次のマイナーを見つけます。 すべての 2 次マイナーが 0 に等しい場合、行列のランクは 1 に等しくなります ( r =1 ).
2. ゼロに等しくない 2 次のマイナーが少なくとも 1 つある場合、境界にある 3 次のマイナーを構成します。 3 次の境界マイナーがすべて 0 に等しい場合、行列のランクは 2 に等しくなります ( r =2 ).
3. 3 次の境界マイナーの少なくとも 1 つがゼロに等しくない場合、境界マイナーを構成します。 4 次の境界マイナーがすべて 0 に等しい場合、行列のランクは 3 に等しくなります ( r =2 ).
4. マトリックスのサイズが許す限り、この手順を続けます。
例1.行列の順位を求める
.
解決。 二次の未成年者 
.
境界線をつけてみましょう。 未成年者は次の 4 人になります。
,
,
したがって、3 次の境界マイナーはすべて 0 に等しいため、この行列のランクは 2 に等しくなります ( r =2 ).
例2。行列の順位を求める
解決。 この行列のすべての 2 次マイナーが 0 に等しいため、この行列のランクは 1 に等しくなります (この場合、次の 2 つの例の境界にあるマイナーの場合と同様に、親愛なる学生は、次のことを確認するよう招待されています)おそらく行列式を計算するためのルールを使用して)、一次マイナーの中、つまり行列の要素の中には、ゼロ以外のものが存在します。
例 3.行列の順位を求める
解決。 この行列の 2 次マイナーは であり、この行列の 3 次マイナーはすべて 0 に等しくなります。 したがって、この行列のランクは 2 です。
例4.行列の順位を求める
解決。 この行列の唯一の 3 次マイナーが 3 であるため、この行列のランクは 3 です。
初等変換法 (ガウス法) を使用して行列のランクを求める
すでに例 1 で、境界マイナー法を使用して行列のランクを決定するタスクには、多数の行列式の計算が必要であることが明らかです。 ただし、計算量を最小限に抑える方法があります。 この方法は基本行列変換の使用に基づいており、ガウス法とも呼ばれます。
次の操作は、基本的な行列変換として理解されます。
1) 行列の行または列にゼロ以外の数値を乗算する。
2) 行列の任意の行または列の要素に、別の行または列の対応する要素を加算し、同じ数を掛けます。
３）行列の２つの行または列を交換する。
4) 「null」行、つまり要素がすべて 0 に等しい行を削除します。
5) 1 つを除くすべての比例線を削除します。
定理。基本的な変換中、行列のランクは変化しません。 言い換えれば、行列からの基本的な変換を使用すると、 あマトリックスに行きました B、 それ 。
